Nice problems (Part 01)

Today, I encountered another interesting mathematical problem again. However, it is so annoying to title posts for each such problem and I don’t believe the list of these problems will have a stop point. Therefore, I decide to collect them into one place for convenience. That is also the reason for this new post series.

The problem is as follows (See Figure 1):

Let $\Delta ABC$ be a right triangle at $A$ such that $\angle{ABC}, \angle{ACB} > \frac{\pi}{6}$. Take two points $D$ and $E$ on the segments $AB$ and $AC$ respectively such that $\angle{BCD} = \angle{CBE} = \frac{\pi}{6}$. Prove that $\angle{ADE} = 3\angle{ABE}$ and $\angle{AED} = 3\angle{ACD}$.

Figure 1. The illustration of the problem.

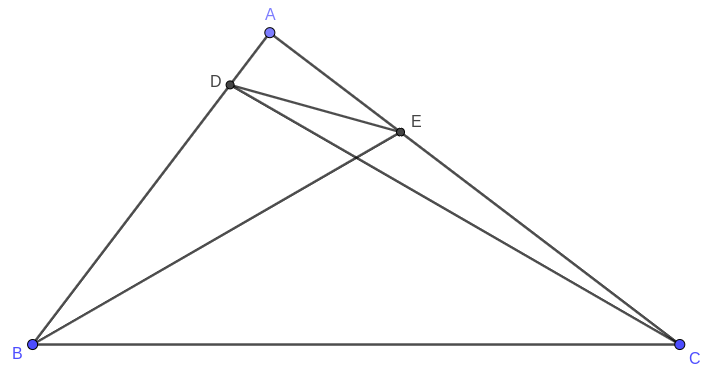
The interesting point of the problem lies in not only its simplicity, but also the ways how it can be solved. More specifically, I present two solutions, one based on geometry and one based on trigonometry. However, the geometric approach is more complex than the trigonometric one, thus the trigonometric one is introduced first.

The trigonometric proof

We have:

\[\begin{aligned} \tan{\angle{ADE}} &= \frac{AE}{AD} \\ &= \frac{AB\tan{\angle{ABE}}}{AC\tan{\angle{ACD}}} \\ &= \frac{\tan{\angle{ABE}}}{\tan{\angle{ACD}} \cdot \tan{\angle{ABC}}} \\ &= \frac{\tan{\angle{ABE}}}{\tan{\left(\frac{\pi}{6} - \angle{ABE}\right)} \cdot \tan{\left(\frac{\pi}{6} + \angle{ABE}\right)}} \\ &= \frac{3\tan{\angle{ABE}} - \tan^3{\angle{ABE}}}{1 - 3\tan^2{\angle{ABE}}} \\ &= \tan{\left(3\angle{ABE}\right)} \end{aligned}\]

Because $0 < \angle{ADE} < \frac{\pi}{2}$ and $0 < \angle{ABE} < \frac{\pi}{6}$, we infer that $\angle{ADE} = 3\angle{ABE}$.

Besides, $\angle{ADE} + \angle{AED} = 3\left(\angle{ABE} + \angle{ACD}\right) = \frac{\pi}{2}$, thus we also infer that $\angle{AED} = 3\angle{ACD}$.

Note: From the problem, especially its trigonometric proof, it is easy to see the trigonometric relation between triple angles and ones of $\frac{\pi}{6}$ and $\frac{\pi}{3}$. Meanwhile, it is not straightforward to spot the presence of the angles of $\frac{\pi}{6}$ and $\frac{\pi}{3}$ when considering the original trigonometric triple-angle formulas. By combining the geometric proof presented next, we have another way to prove those formulas.

The geometric proof

Before starting, I need to add a circle, some lines and points to the original figure: Let $(O)$ be the circumscribed circle of $\Delta ABC$. Then, $I$ and $J$ are respectively the intersections between $(O)$ and the lines $CD$ and $BE$. Next, $G$ and $H$ are respectively the projections of $D$ and $E$ onto the line $BC$. After that, $AG$ intersects $(O)$ in $M$, $AH$ intersects $(O)$ in $N$, $AB$ intersects $IM$ in $P$, $AC$ intersects $JN$ in $Q$. Finally, the result obtained is shown in Figure 2.

Figure 2. The illustration for the geometric proof.

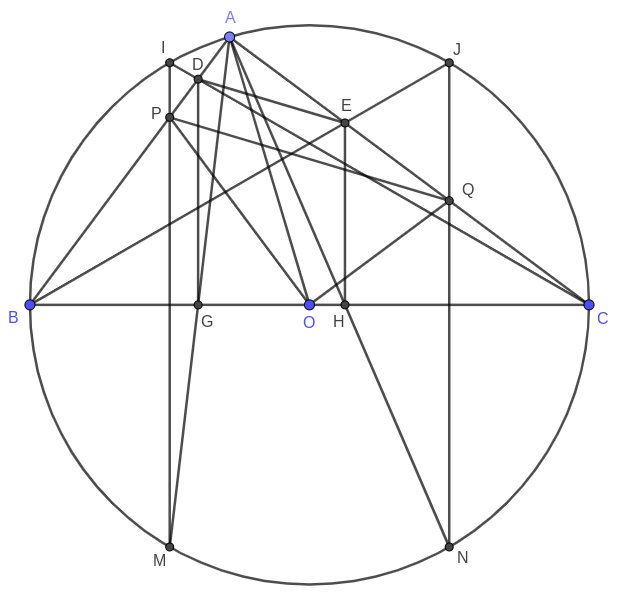
The first thing need to prove is $IM \perp BC$ and $JN \perp BC$: We have $ADGC$ and $AEHB$ are inscribed quadrilaterals, thus $\angle{BAM} = \angle{BCI}$ and $\angle{CAN} = \angle{CBJ}$. Therefore, it is quite easy to infer that $M$ and $N$ are respectively the reflections of $I$ and $J$ through the line $BC$. Hence, $IM \perp BC$ and $JN \perp BC$.

Because $IM \perp BC$ and $JN \perp BC$, we infer that $IM \parallel DG \parallel EH \parallel JN$. Therefore, we have $\frac{AD}{AP} = \frac{AG}{AM}$ and $\frac{AE}{AQ} = \frac{AH}{AN}$.

Because $\angle{BCD} = \angle{CBE} = \frac{\pi}{6}$, we can prove that $IJ \parallel BC$. In addition, $M$ and $N$ are respectively the reflections of $I$ and $J$ through the line $BC$, so $MN \parallel BC$. From that, we have $\frac{AG}{AM} = \frac{AH}{AN}$. Combining with $\frac{AD}{AP} = \frac{AG}{AM}$ and $\frac{AE}{AQ} = \frac{AH}{AN}$, we have $\frac{AD}{AP} = \frac{AE}{AQ}$, which implies that $DE \parallel PQ$. Hence, $\angle{ADE} = \angle{APQ}$ and $\angle{AED} = \angle{AQP}$.

Thanks to $\angle{BCD} = \angle{CBE} = \frac{\pi}{6}$, $IM \perp BC$, and $JN \perp BC$, we can also prove that $B$ and $C$ are respectively the reflections of $O$ through the lines $IM$ and $IN$. Thus, we can infer that $\angle{POQ} = \frac{\pi}{2}$, so $APOQ$ is an inscribed quadrilaterals. Therefore, we have:

\[\begin{aligned} \angle{ADE} &= \angle{APQ} \\ &= \angle{AOQ} \\ &= \pi - \angle{OAQ} - \angle{OQA} \\ &= \pi - \angle{BCA} - 2\angle{BCA} \\ &= 3\angle{CBA} - \frac{\pi}{2} \\ &= 3\angle{ABE} \\ \angle{AED} &= \angle{AQP} \\ &= \angle{AOP} \\ &= \pi - \angle{OAP} - \angle{OPA} \\ &= \pi - \angle{CBA} - 2\angle{CBA} \\ &= 3\angle{BCA} - \frac{\pi}{2} \\ &= 3\angle{ACD} \\ \end{aligned}\]

Note: Although my above proof is true, I still believe there is a proof more simple than mine. Hope you, the readers, can find it for me :))