Theory of Relativity (Part 01)

Most people know Albert Einstein and his very famous works relating to the Theory of Relativity, especially the equation:

\[E = mc^2\]

This equation is the foundation for numerous discoveries, including the development of nuclear bombs, the most destructive weapon ever created. For me, the equation holds a beauty akin to Euler’s equation $e^{i \pi} = -1$. The curiosity about how Einstein derived it motivates me to delve deeper into his theories of relativity, and it’s the very reason this series of notes is born.

The Theory of Relativity contains two sub-theories: Special Relativity and General Relativity, proposed by Einstein in 1905 and 1915 respectively. Following the historical order, the first notes in the series will focus on Special Relativity, with the two most important postulates:

1. The principle of relativity: The laws of physics take the same form in all inertial frames of reference.
2. The invariance of $c$: The speed of light in free space has the same value $c$ in all inertial frames of reference.

Based on the two postulates above, we can derive the first result in Special Relativity - the Lorentz transformation.

Considering two inertial frames $F$ and $F’$ that satisfy the following requirements:

• They use the same units of time and length.
• An event occurs at the origin $O$ at time $t = 0$ in $F$ if and only if it also occurs at the origin $O’$ at time $t’ = 0$ in $F’$.
• $Ox$, $Oy$, and $Oz$ are respectively in the same positive directions as $O’x’$, $O’y’$, and $O’z’$.

Assume that $O’$ is moving along $x$-axis with velocity $v$ in $F$. Note that both $F$ and $F’$ is inertial, so $v$ is constant. Without loss of generality, assume that $v > 0$.

Then, we have the following remarks:

– $F’$ moves only along the $x$-axis of $F$, and vice versa. Therefore, the $y$ and $z$ coordinates of a point in $F$ should be the same as the corresponding $y’$ and $z’$ coordinates in $F’$.

\[\begin{aligned} y' &= y \\ z' &= z \\ \end{aligned}\]

– Any object moving along $x$-axis with velocity $v$ in $F$ remains at rest in $F’$.

\[x = x_0 + vt \iff x' = x'_0 = const\]

Therefore, $x = vt \iff x’ = 0$.

– Photons must move with the same velocity $c$ in both $F$ and $F’$ due to the second postulate. Therefore, assume that there exists a photon at the origin $O$ at time $t = 0$ in $F$, moving along $x$-axis in positive direction.

\[x = ct \iff x' = ct'\]

Then, at time $t = t_1$ in $F$, the photon is reflected and moves back along the $x$-axis.

\[\begin{aligned} x &= x_1 - c(t - t_1) = (x_1 + ct_1) - ct = 2ct_1 - ct \\ \iff x' &= x'_1 - c(t' - t'_1) = (x'_1 + ct'_1) - ct' = 2ct'_1 - ct' \\ \end{aligned}\]

Next, at time $t = t_2$ in $F$, the photon arrives at the origin $O’$ moving along $x$-axis with velocity $v$ in $F$. Therefore, at time $t = t_2$ in $F$, both the photon and the origin $O’$ are at the same place.

\[\begin{aligned} x_2 &= 2ct_1 - ct_2 = c(2t_1 - t_2) \\ &= vt_2 \\ \implies t_2 &= \frac{2c}{c + v} t_1 \\ \end{aligned}\]

In addition, both the photon and the origin $O’$ are also at the same place at time $t’ = t’_2$ in $F’$.

\[\begin{aligned} x'_2 &= 2ct'_1 - ct'_2 = c(2t'_1 - t'_2) \\ &= 0 \\ \implies t'_2 &= 2t'_1 \\ \end{aligned}\]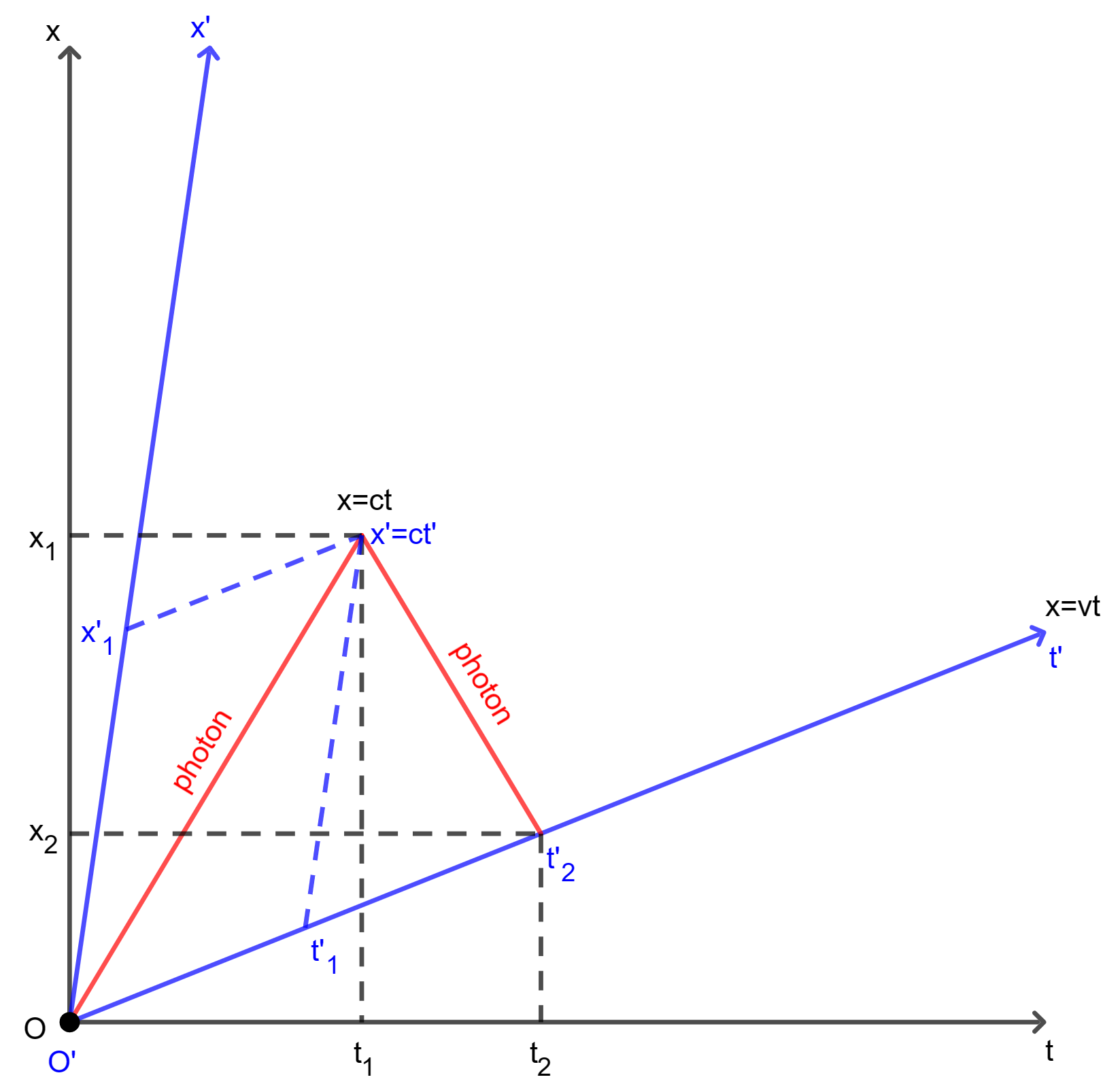

Figure 1. A photon moves, then is reflected and moves back in both $F$ and $F’$.

The whole process is illustrated in Figure 1. Thus, at time $t = \frac{t_2}{2} = \frac{c}{c + v} t_1$ in $F$, the corresponding time at the origin $O’$ in $F’$ is $t’ = \frac{t’_2}{2} = t’_1$. However, $t’ = t’_1$ is also the time that the photon is reflected in $F’$. So, we can imply that the following events occur at the same time $t’ = t’_1$ in $F’$.

• The event that the origin $O’$ is at time $t = \frac{c}{c + v} t_1$ in $F$.

\[\begin{cases} x = \frac{cv}{c + v} t_1 \\ t = \frac{c}{c + v} t_1 \\ \end{cases}\]

• The event that the photon is reflected in $F$.

\[\begin{cases} x = ct_1 \\ t = t_1 \\ \end{cases}\]

Then, given $0 \leq \alpha, \beta \leq 1$ and $\alpha + \beta = 1$, when a photon is reflected at time $t’ = t’_1$ after passing the origin $O’$ at time $t’ = \alpha t’_1$ in $F’$, the event occurs in $F$ as follows:

\[(x, t) = \left[\alpha \left(\frac{cv}{c + v}, \frac{c}{c + v}\right) + \beta (c, 1)\right] t_1\]

All events having the above form occur at the same time $t’ = t’_1$ in $F’$. That means they establish the positive $O’x’$-axis in $F’$. Therefore, the set of events occuring on the positive $O’x’$-axis at time $t’ = 0$ in $F’$ is $x = \frac{c^2}{v} t$.

– The set of events occuring only at the origin $O’$ in $F’$ is $x = vt$.

– In conclusion, if $(x, t) = \left(\frac{c^2}{v}, 1\right)$ corresponds to $x’ = \theta_x > 0$ and $(x, t) = (v, 1)$ corresponds to $t’ = \theta_t > 0$, then we have the following transformation:

\[\begin{aligned} &\begin{pmatrix} x \\ y \\ z \\ t \\ \end{pmatrix} = \begin{pmatrix} \frac{c^2}{v} \\ 0 \\ 0 \\ 1 \\ \end{pmatrix} \frac{x'}{\theta_x} + \begin{pmatrix} v \\ 0 \\ 0 \\ 1 \\ \end{pmatrix} \frac{t'}{\theta_t} + \begin{pmatrix} 0 \\ y' \\ z' \\ 0 \\ \end{pmatrix} \\ \iff & \begin{cases} x' = \frac{v}{c^2 - v^2} \theta_x (x - vt) \\ y' = y \\ z' = z \\ t' = \frac{c^2}{c^2 - v^2} \theta_t \left(t - \frac{vx}{c^2}\right) \\ \end{cases} \end{aligned}\]

Then, by the second postulate, the velocity of photons in $F$ and $F’$ are the same.

\[x^2 + y^2 + z^2 = c^2 t^2 \iff x'^2 + y'^2 + z'^2 = c^2 t'^2\]

So, we can imply that:

\[\begin{aligned} & x^2 - c^2 t^2 = x'^2 - c^2 t'^2 \\ \iff & \left(\frac{v^2 (\theta_x^2 - c^2 \theta_t^2)}{(c^2 - v^2)^2} - 1\right) x^2 - \frac{2v (v^2 \theta_x^2 - c^4 \theta_t^2)}{(c^2 - v^2)^2} xt + \left(c^2 + \frac{v^4 \theta_x^2 - c^6 \theta_t^2}{(c^2 - v^2)^2}\right) t^2 = 0 \\ \end{aligned}\]

The equation holds for all $x$ and $t$, so we imply that:

\[\begin{aligned} & \begin{cases} v^2 (\theta_x^2 - c^2 \theta_t^2) = (c^2 - v^2)^2 \\ v^2 \theta_x^2 = c^4 \theta_t^2 \\ c^2 (c^2 - v^2)^2 + v^4 \theta_x^2 - c^6 \theta_t^2 = 0 \\ \end{cases} \\ \iff & \begin{cases} \theta_x^2 = \frac{c^2 (c^2 - v^2)}{v^2} \\ \theta_t^2 = \frac{c^2 - v^2}{c^2} \\ \end{cases} \end{aligned}\]

In addition, $\theta_x > 0$ and $\theta_t > 0$.

\[\begin{cases} \theta_x = \frac{c \sqrt{c^2 - v^2}}{v} \\ \theta_t = \frac{\sqrt{c^2 - v^2}}{c} \\ \end{cases}\]

Therefore, the Lorentz transformation is as follows:

\[\begin{cases} x' = \gamma (x - vt) \\ y' = y \\ z' = z \\ t' = \gamma \left(t - \frac{vx}{c^2}\right) \\ \end{cases}\]

where $\gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}}$ is the Lorentz factor.