Merkle tree

There are so many articles about this topic, so I don’t want to repeat what others wrote. In this post, I will try to focus things related to my work.

Before starting, I will talk briefly about the concept of Merkle trees. Basically, Merkle trees are binary trees. The main difference is that the value of every node in Merkle trees is created by applying cryptographic hash functions to: the value of child nodes (for interior nodes) and the value of data blocks (for leaves).

Figure 1 is a Merkle tree with 4 data blocks. You can read more about the description of this Merkle tree in this link. Perhaps now we are wondering why we need Merkle trees, what they can do, or what is special about them.

Figure 1. An example of a Merkle tree. (Source: Wikipedia)

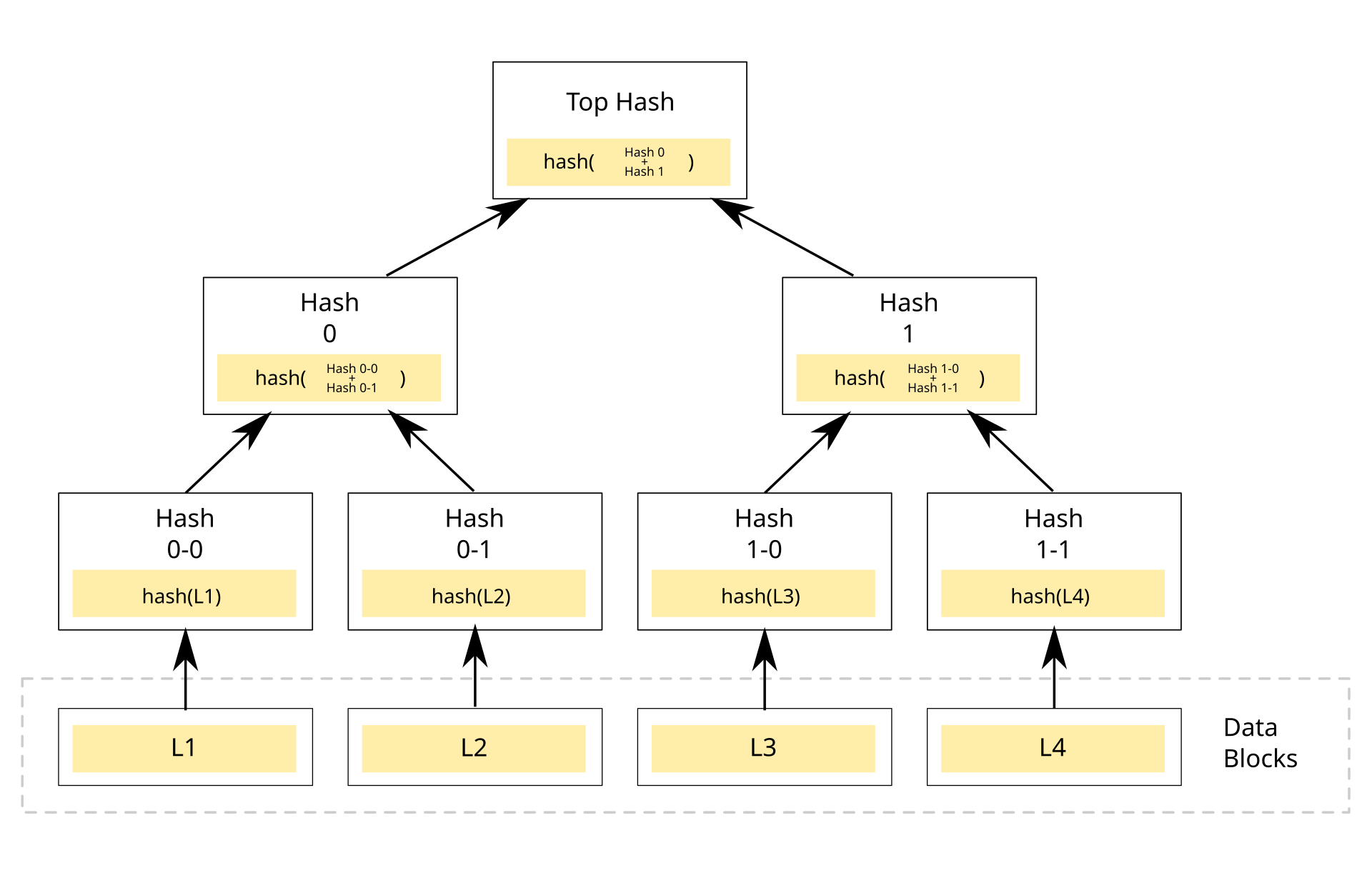
Before answering above questions, we need to remember that cryptographic hash functions are used for data integrity checks. Thanks to the properties of pre-image resistance, second pre-image resistance, and collision resistance, it is considered hard to find another value having the same hash with a given value. Therefore, a Merkle tree is one of multiple ways to check data integrity. For example, in Figure 1, if we have the value of the top hash, we can easily check the integrity of all 4 data blocks.

However, the interesting thing about Merkle trees is not only that. They also allow to check the integrity of an arbitrary data block based on $\log(N)$ hash values if we assume that there are $N$ data blocks. More specific, we revisit the example in Figure 1. To check the integrity of the block L2, we just need the values of the hash 0-0, and the hash 1 to recover the value of the top hash. In a similar way, we can check the integrity of the block L3 with the values of the hash 1-1, and the hash 0. So, in all cases, we only need $\log(4) = 2$ hash values to check the integrity of a data block.

From the above example, we find out this is also a beautiful way to check the membership and the order of an identity number. Based on the value of the top hash and the way it is created, we can idetify if a person is in an organization and what is the order of that person if true. Broadly speaking, if we can combine it with commitment schemes and zero knowledge proofs, a Merkle tree shows its potential when it can significantly reduce the computational cost, especially in the set membership and non-membership problems. This is the topic I am recently interested in, and I am very happy to share with everyone.

Have a nice day!