The closest point

Today’s problem is derived from a memory about a programming lesson I learned when I was a freshman. It is stated as follows:

Given the coordinates of three vertices of a triangle, find the coordinates of a point such that sum of the three distances from that point to each of these vertices is the smallest.

At that time, there was two opinions about the solution of this problem. Some of my classmates supposed that the point we needed to find was the centroid of the triangle, while some people said that was not true. Nobody could provide the proof for their claims. Therefore, I decided to find the answer myself.

…

At present, for me, although the problem is not difficult anymore, it is still interesting. I will not provide a detailed solution because you can find it easily on the Internet. Of course, that point is not the centroid of the triangle. It is called the Fermat point of the triangle. However, I will leave some figures I used to solve in case you also find the problem interesting like me.

Figure 1. Finding the point I satisfying the requirements of the problem.

Figure 2. Proving AA’, BB’, CC’ are concurrent.

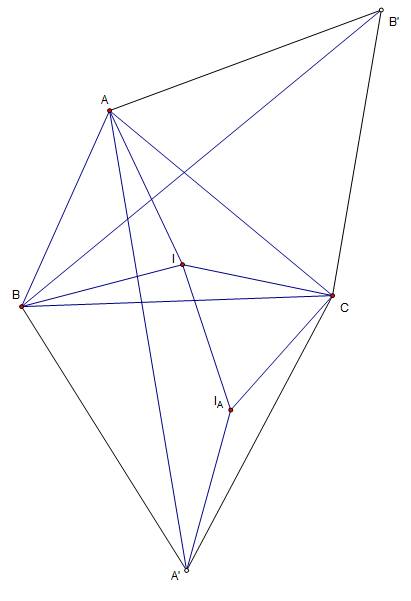
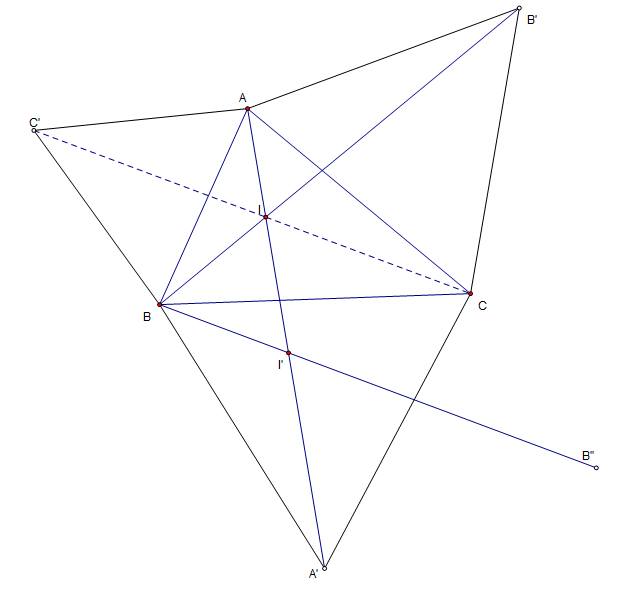
Note: Sorry for the low quality of the figures, but I really want to keep their originals.

For readers, can you solve the more general problem where the triangle is replaced by a polygon?

Hint

The main technique I used is rotation. By applying rotation, I can use a important property: isometry.

In Figure 1, the triangles BCA', ACB', and ICI_A are equilateral triangles.

In Figure 2, the triangles ABC', BCA', CAB', and BB'B" are equilateral triangles. Besides, I is the intersection point of AA' and BB', while I' is the intersection point of AA' and BB".