Just a fun problem

A few day ago, I came across a mathematical problem by accident on the Internet. It was described as Figure 1 without any further explanations.

Figure 1. The original problem.

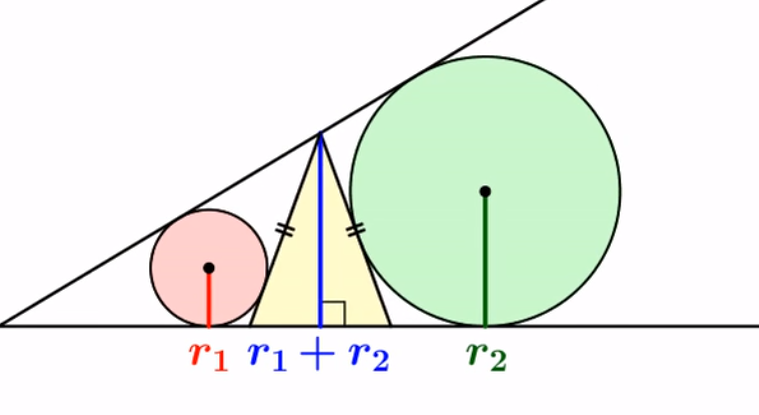
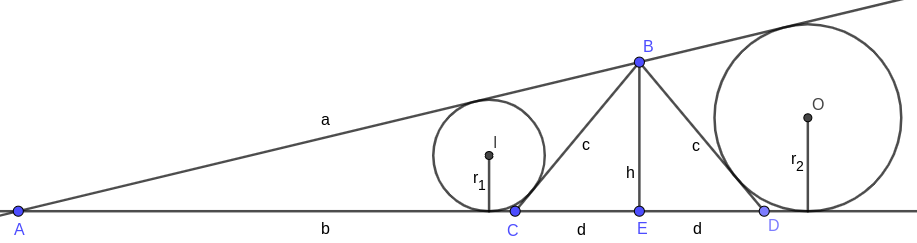
To make it more clear, I redraw it as shown in Figure 2 and assume that $(I, r_1)$ is the incircle of the triangle $ABC$ and $(O, r_2)$ is the $A$-excircle of the triangle $ABD$.

Figure 2. Redrawing and formalizing the problem.

You can try to solve it yourself before reading the below solution.

---

Solution. We have the following results:

\[\begin{aligned} S_{ABC} &= \frac{1}{2} r_1 (AB + BC + CA) = \frac{1}{2} BE \cdot AC \\ S_{ABD} &= \frac{1}{2} r_2 (AB - BD + DA) = \frac{1}{2} BE \cdot AD \\ \end{aligned}\]

If we let $AB = a$, $AE = b$, $BC = BD = c$, $EC = ED = d$, and $BE = h$, we have:

\[\begin{aligned} \frac{r_1 + r_2}{BE} &= \frac{AC}{AB + BC + CA} + \frac{AD}{AB - BD + DA} \\ &= \frac{b - d}{a + c + b - d} + \frac{b + d}{a - c + b + d} \\ &= 2 \frac{ab + b^2 + cd - d^2}{(a + c + b - d)(a - c + b + d)} \\ &= 2 \frac{ab + b^2 + cd - d^2}{(a + b)^2 - (c - d)^2} \\ &= 2 \frac{ab + b^2 + cd - d^2}{a^2 + 2ab + b^2 - c^2 + 2cd - d^2} \\ &= 2 \frac{ab + b^2 + cd - d^2}{(b^2 + h^2) + 2ab + b^2 - (d^2 + h^2) + 2cd - d^2} \\ &= 1 \\ \end{aligned}\]

Therefore, $h = BE = r_1 + r_2$.